Tutoriales
Enlaces
Licencia

Esta obra está bajo una licencia de Creative Commons.
Para reconocer la autoría debes poner el enlace https://old.chuidiang.org

Como muchas veces en este tipo de problemas, suponemos el problema resuelto y vamos a tratar de buscar cosas en los puntos medios del pentágono.
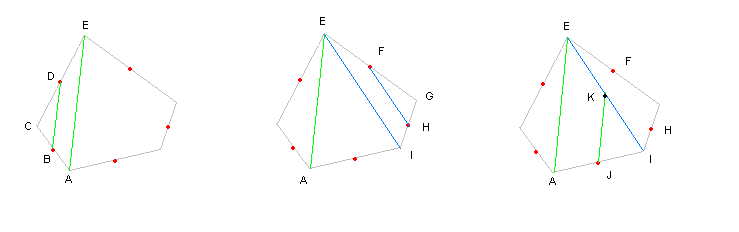
En la figura nos fijamos en el primer pentágono. Según el enunciado del problema, B es el punto medio entre C y A, por lo que CA es el doble que CB. De la misma forma, CE es el doble que CD. Si nos fijamos en los triángulos EAC y DBC, por semejanza de triángulos, el lado EA debe ser el doble de BD y deben ser paralelos.
En el segundo pentágono y de la misma forma, vemos que el triángulo EGI es el doble que el FGH y que el lado EI es el doble que el FH y son paralelos.
Nos fijamos ahora, en el tercer pentágono, en el triángulo EIA. Si trazamos desde J una linea paralela a AE, cortamos a EI en el punto K. Fijemonos en los dos triángulos que hemos obtenido: EIA y KIJ. Puesto que J según el enunciado es el punto medio entre I y A, el triángulo EIA es el doble que el KIJ. Por ello, KJ es la mitad que EA, y por tanto KJ coincide con BD. De la misma forma, el lado EI del triángulo grande es el doble que el lado KI del pequeño, por lo que KI coincide con FH.
Volvamos ahora al problema sin resolver.
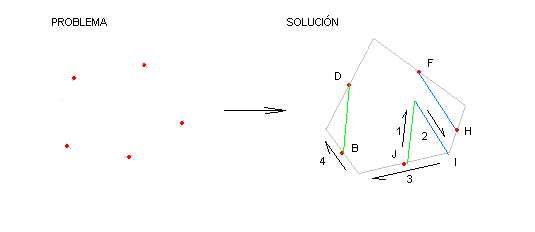
Según lo que hemos sacado, base con llevarse a partir del punto J el lado BD (linea 1 del dibujo, según la flecha). Sobre el extremo, llevamos ahora el lado FH (línea 2 del dibujo, según la flecha) y así obtenemos el vértice I del pentágono. El resto es sencillo, basta unir I con J y prolongar otro tanto para obtener el siguiente vértice (línea 3 del dibujo según la flecha) y así sucesivamente (línea 4, ...).
Curiosamente este procedimiento vale para cualquier polígono de un número impar de lados. Podemos, por ejemplo, hablar del problema de los 11 paracaidistas...